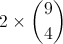Ytterligare tre dystopiska actionrullar avklarade: Oblivion, Elysium och World War Z.
Det är lite som schlagerfestivalen, det där med att läsa recensioner (NYT, SvD, GP, UNT, HD, m.fl.). Hur luttrad man än är, så blir man likväl förvånad över hur tolkningar och tyckanden spretar - både inbördes och i jämförelse med ens egna.
Ingen av filmerna är värd att skriva en uppsats om, men mycket kort kan sägas att Oblivion kan hoppas över; Elysium är intressant men övertygar tyvärr inte. (Är det inte dags att Matt Damon gör något riktigt bra snart?)
World War Z är (vilket förvånade mig) mest sevärd, av flera skäl: Produktionen är i särklass den mest gedigna, alla kategorier. Berättandet är, om inte originellt, så åtminstone uppfriskande. Som skräck-action är den nästan onödigt bra (även om vissa typiska skräckfilmsbrister kvarstår). Men framför allt: de stråk av allvar och budskap som kan skönjas är smarta och subtila (ja, bortsett från elefanten i rummet). Ironiskt, då, att drakarna beslår Elysium med övertydlighet (för att inte tala om SvD:s bisarra läsning), men att ingen av dem ser något mer än zombies i World War Z.
Dagens ord
Ansvar väger tyngre än frihet - Responsibility trumps liberty
29 dec. 2013
14 dec. 2013
Observationens teoriberoende, revisited
Consider the laudable, but now somewhat tarnished initiative to establish evidence-based policymaking. What went wrong? All too often, objective evidence was taken to be data uncontaminated by the bias of a prior theory. But without "the very soul" of a theory as guidance, what constitutes evidence? Objectivity isn't to do with with stripping out all presuppositions. Indeed, the more that's considered possible or desirable, the greater the undetected, uncriticized presuppositions and the less the objectivity. At worst, a desired but unstated goal can be smuggled in at the outset. And the upshot? This well-meant approach is often justifiably derided as "policy-based evidence-making".
Helena Cronin: In the beginning is the theory
I Brockman (red.), This explains everything, s. 157
7 dec. 2013
Problemlösning med progression
Jag hittade en uppgift på Mattecentrums Facebooksida:
Kan du arrangera siffrorna 1-9 i en cirkel så att summan av alla sifferpar ej är delbara med 3, 5 och 7?
Jag gav mina pojkar, 7 och 10 år, i uppgift att lösa den. Det var mycket instruktivt att se och höra dem gripa sig an problemet. Jag tittade också på kommentarerna på Mattecentrums sida, och det visade sig även där att redan TOLKNINGEN av uppgiften ger upphov till många problem.
Min äldste grabb behövde inte mycket stöttning för att komma igång. Efter hand utvecklade han själv flera systematiska sätt att närma sig en lösning. Han kom fram till en kedja av 6 siffror som alla uppfyllde villkoret, men stötte sedan på patrull, då det finns flera sätt att ta fram en sådan, men endast en (eller ett fåtal) som kan leda hela vägen till en cirkel med nio siffror.
Lillkillen och jag använde Excel för att ta fram en tabell över alla möjliga summor, och sedan stryka de summor som inte uppfyller villkoret. Sedan hade vi en god översikt över vilken väg vi kunde ta mot målet. Under tiden gjorde tioåringen något likande med papper och penna: Han skev upp alla summor mellan 3 och 18 och strök sedan dem som var delbara med 3, 5 och 7.
När vi var klara, pratade vi om primtal, och om tal som innehåller faktorn 2 och andra faktorer skilda från 3, 5 och 7.
Så det finns utrymme för progression här.
Men det viktigaste är nog dels TOLKNINGEN, som sagt, och att förelägga sig en fungerande SYSTEMATIK i sitt sökande efter lösning.
Kan du arrangera siffrorna 1-9 i en cirkel så att summan av alla sifferpar ej är delbara med 3, 5 och 7?
Jag gav mina pojkar, 7 och 10 år, i uppgift att lösa den. Det var mycket instruktivt att se och höra dem gripa sig an problemet. Jag tittade också på kommentarerna på Mattecentrums sida, och det visade sig även där att redan TOLKNINGEN av uppgiften ger upphov till många problem.
Min äldste grabb behövde inte mycket stöttning för att komma igång. Efter hand utvecklade han själv flera systematiska sätt att närma sig en lösning. Han kom fram till en kedja av 6 siffror som alla uppfyllde villkoret, men stötte sedan på patrull, då det finns flera sätt att ta fram en sådan, men endast en (eller ett fåtal) som kan leda hela vägen till en cirkel med nio siffror.
Lillkillen och jag använde Excel för att ta fram en tabell över alla möjliga summor, och sedan stryka de summor som inte uppfyller villkoret. Sedan hade vi en god översikt över vilken väg vi kunde ta mot målet. Under tiden gjorde tioåringen något likande med papper och penna: Han skev upp alla summor mellan 3 och 18 och strök sedan dem som var delbara med 3, 5 och 7.
När vi var klara, pratade vi om primtal, och om tal som innehåller faktorn 2 och andra faktorer skilda från 3, 5 och 7.
Så det finns utrymme för progression här.
Men det viktigaste är nog dels TOLKNINGEN, som sagt, och att förelägga sig en fungerande SYSTEMATIK i sitt sökande efter lösning.
17 nov. 2013
God natt
Jag vilar trygg uti mitt bo
I sällsam bädd av barnatro
Att runt omkring och just i dag
Är allt som sker just som det ska
I sällsam bädd av barnatro
Att runt omkring och just i dag
Är allt som sker just som det ska
10 nov. 2013
Insomnia
Jag vaknade och steg ut i drömmen
Lät mig fjärrstyras genom dagen
Kände livsviljan bölja fram och tillbaka
och undrade vems den var
En marionett-teater
Tablåer i tablåer
Tjattrande dockor
på scenen; framför; bakom
En babusjka letar vila
Lägger pussel
söker ro
Mitt inre fryser utan skal
Döden skrämmer mig
retar mig
Utmattade skärvor
gungar svagare
Trevar sig sakta mot varandra
under natten
Något, någon
sköljs upp i dagen
Famlar efter form
15 sep. 2013
Kuratorn är den nya pedagogen
Så här i MOOC:ernas tidevarv (Massively Open Online Courses), med flippade klassrum även i grundskolan, växer en ny näringskedja fram.
En del pedagoger blir innehållsskapare - och flyttar alltså upp ett snäpp i kedjan.
En del blir kuratorer - i bemärkelsen "curator", föreståndare för museiverksamhet - och flyttar därmed upp två snäpp.
När jag ser en fantastisk filmad föreläsning (som t.ex. den här) av en svårslagen innehållsskapare, och ödmjukad funderar över mitt eget existensberättigande, finner jag tröst i tanken att jag åtminstone är en av de första (?) kuratorerna i denna sköna nya värld.
En del pedagoger blir innehållsskapare - och flyttar alltså upp ett snäpp i kedjan.
En del blir kuratorer - i bemärkelsen "curator", föreståndare för museiverksamhet - och flyttar därmed upp två snäpp.
När jag ser en fantastisk filmad föreläsning (som t.ex. den här) av en svårslagen innehållsskapare, och ödmjukad funderar över mitt eget existensberättigande, finner jag tröst i tanken att jag åtminstone är en av de första (?) kuratorerna i denna sköna nya värld.
Kombinatorik och Kaizen
En riksdagsledamot har 10 stycken vänner i riksdagen. Hon vill bjuda in fyra av dessa vänner till en gemensam middag, men vet också att hon inte kan bjuda in de båda vännerna Amanda och Benjamin samtidigt, eftersom dessa inte kommer överens med varandra.
På hur många sätt kan hon välja fyra av de tio vännerna, utan att hon väljer både Amanda och Benjamin?
Den här uppgiften är hämtad från Mattekampen 2013, ett initiativ av Mattecentrum.
Uppgiften är ett exempel på kombinatorik, som i sin tur är en gren av diskret matematik.
Den är svår - ovanligt svår för att ingå i ett test för riksdagspolitiker. Ja, svår även för de flesta som precis har gått ut gymnasiet. Eller högskolan, för den delen. Svår t.o.m. för de - få - som faktiskt läser, eller har läst, just diskret matematik (på gymnasiet).
Mitt syfte med den här texten är att särskilt lyfta fram en av orsakerna till varför uppgiften uppfattas som svår (det finns flera).
En kollega och jag roade oss med att diskutera uppgiften över en öl en fredag eftermiddag efter jobbet. Och redan här finns flera ledtrådar: Vissa människor tycker uppenbarligen att sådana här problem är roliga! Samtidigt - ja, samtidigt - kan de upplevas som krävande, skrämmande och frustrerande. För många människor, och detta inkluderar matematiker och matematiklärare - är de enbart frustrerande.
För någon som är van vid att lösa den här typen av problem är mycket givet på förhand: Man vet vilka metoder som ska användas, och man vet dessutom hur och varför dessa metoder fungerar. Trots detta är vägen till en lösning inte självklar. Värre än så: huruvida en färdig lösning faktiskt är korrekt är också ofta långt ifrån självklart. Så mycket värre för någon som tvingas resonera sig fram till en lösning utan tillgång till färdiga metoder.
Här följer några exempel på lösningar, utförda med hjälp av standardmetoder.
A. En ska bort
Om man först plockar bort Amanda, på hur många sätt kan man då välja fyra personer av de nio som återstår? Låt oss kalla svaret på den frågan för C(9, 4). Ingen av dessa sällskap innehåller både Amanda och Benjamin, eftersom Amanda inte är med i urvalet. På samma sätt, om man först plockar bort Benjamin kan man bilda C(9, 4) sällskap utan honom. Totalt har man alltså 2 × C(9, 4) möjligheter. Eller, med en annan notation:
B. Båda ska bort
Om man först plockar bort både Amanda och Benjamin kan man av de återstående åtta personerna bilda C(8, 4) sällskap. Men då har man ju inte räknat med de möjligheter där någon (endast en) av de två ovännerna ingår. Hur många sådana finns? Jo, om man i stället för att plocka bort Amanda börjar med att bestämma sig för att hon ska ingå i sällskapet, då har man bara tre personer kvar att välja. Men inte av nio återstående personer, utan av åtta - eftersom Benjamin då inte får väljas. Alltså har man C(8, 3) möjligheter. På samma sätt med Benjamin: det finns C(8, 3) möjligheter att välja ett sällskap där han garanterat ingår och där Amanda garanterat inte ingår. Vi har nu alltså först räknat de sällskap där ingen av ovännerna ingår; sedan de sällskap där Amanda ingår (men inte Benjamin); och slutligen de sällskap där Benjamin ingår (men inte Amanda). Har vi räknat alla möjligheter då? Ja, det har vi. Alltså:
Bry dig inte om hur vi får fram värdet 182 just nu. Det kommer vi till längre fram. Det viktiga nu är själva resonemanget, och att det skiljer sig från det resonemang vi förde i A.
C. Ingen ska bort (förrän i efterhand)
Hur många möjligheter finns om man inte bryr sig om att plocka bort någon av ovännerna? Jo, C(10, 4) Då har man alltså räknat alla möjliga sällskap, även dem där både Amanda och Benjamin ingår. Och de måste ju räknas bort. Så hur många är de? Låt oss räkna "baklänges": Alla de möjliga sällskap där båda ovännerna ingår skulle vi kunna bilda genom att först välja ut just dessa två och bestämma att de ska ingå. Då saknas två personer för att sällskapet ska bli fulltaligt. På hur många sätt kan vi då välja dessa två, av de åtta personer som då återstår? Jo, C(8, 2). Nu har vi först räknat alla möjliga sällskap, och sedan dragit bort dem som inte fungerar:
Vi får samma svar i både B och C, vilket är uppmuntrande. Vilken av dessa två tycker du verkar rimligast? Båda? Ingen? Känns någon av dem rimlig, men fortfarande inte helt övertygande? Eller är båda helt övertygande? Och undrar du i så fall hur det kan vara så? Blir du kanske lite misstänksam?
Hur är det med lösning A? Den ger svaret:
Aj då... Är det något fel? Eller är det kanske B och C som innehåller något fel? Hur kan vi veta det?
Vi tittar på A igen. Vi har räknat alla de sällskap där Amanda inte ingår, och alla de sällskap där Benjamin inte ingår. Det är väl bra? Finns det några fler? Nej, det gör det väl inte...
Eftersom vi nu har två alternativa lösningar att jämföra med, som båda ger samma svar, och som dessutom ger ett lägre svar, kan vi kanske börja misstänka att vi i A har räknat med för många möjligheter.
A'. En ska bort, men bara en
Alla sällskap där Amanda inte ingår, och alla sällskap där Benjamin inte ingår... Hur är det med de sällskap där ingen av dem ingår? De ingår ju både i mängden av sällskap som inte innehåller Amanda och i mängden av sällskap som inte innehåller Benjamin. (Det kan man se om man t.ex. ritar upp ett s.k. Venn-diagram.) Vi har alltså räknat med dem två gånger när vi lade ihop de sällskap som garanterat inte innehöll en av ovännerna. Vi måste alltså dra bort dem en gång. Hur många möjliga sällskap innehåller inte någon av ovännerna? Det räknade vi ut i B: C(8, 4). Vårt nya lösningsförslag blir alltså:
(Hur kommer man att tänka på detta? Hur kan man lära sig att komma på sådana här saker? Kan man lära sig det?)
(I facit till Mattekampen ges C som lösningsförslag.)
Vilken lösningsmetod hade du valt? Om du hade valt A, hade du då kommit fram till A' ?
Vad hade du gjort om du inte sedan tidigare varit bekant med notationen C(n, k)? Jag tror att det då hade varit mycket svårt, men inte omöjligt, för dig att lösa problemet.
---
Låt oss titta närmare på notationen C(n, k) På hur många sätt kan man välja ut k föremål ur en mängd av n stycken föremål? Alla föremål är unika (d.v.s. det går att göra skillnad på dem). Men det spelar ingen roll i vilken ordning de väljs ut.
Ett exempel: Du har fem inramade foton på dina barn och ska ge bort två av dessa till svärmor i julklapp. På hur många sätt kan du välja ut två av fem foton? (Notera att det spelar ingen roll i vilken ordning du väljer ut dem; det enda viktiga är vilka foton svärmor får.)
Tänk dig att du lägger de fem fotona framför dig på en rad. Det första fotot du väljer kan då vara vilket som helst av de fem. Låt säga att du tar bort detta foto från raden och lägger det i ett paket. Kvar ligger nu fyra foton. Du ska välja ett till, och du har nu fyra möjligheter. Du tar bort ytterligare ett foto, vilket som helst, från raden och placerar det i paketet. Nu är svärmors julklapp klar.
På hur många olika sätt skulle den här scenen kunna utspela sig? Det första fotot kan vara vilket som helst av de fem som ligger framme. Nästa foto kan vara vilket som helst av de fyra återstående. För var och en av de fem första scenariorna, finns det fyra fortsättningar. Du har alltså 5 × 4 = 20 möjligheter att välja ut två foton till svärmor.
Men vänta! För svärmors del spelar det ju ingen roll i vilken ordning du har valt ut fotona. Det enda hon är intresserad av är vilka foton som ligger i paketet. I ett av de tjugo scenariorna ovan väljer du först foto X och därefter foto Y. I ett annat scenario väljer du först foto Y och sedan foto X. Av de tjugo scenariorna är alltså hälften likvärdiga, ur svärmors synvinkel. Det finns alltså bara 20/2 = 10 unika julklappar.
Ovanstående sammanfattar vi så här:
Vilket alltså säger att det finns 10 unika urval av två föremål ur en samling på fem föremål.
Hur många unika julklappar kan svärmor få om paketet innehåller tre, i stället för två, foton? Som tidigare resonerar vi först att det finns 5 × 4 × 3 olika sätt att välja ut de tre fotona.
Sedan måste vi ta hänsyn till att en del av dessa resulterar i samma urval av foton. På hur många sätt kan t.ex. foto X, Y, och Z hamna i samma paket? Jo, X skulle kunna hamna i paketet genom att bli utvalt först, men det skulle också kunna hamna i paketet som nummer två i ordningen, eller som nummer tre. Det finns alltså tre möjligheter för foto X att ingå i paketet. Om foto X väljs ut först, kan foto Y väljas antingen som andra eller som tredje foto i ordningen. För varje plats i ordningen som X får, finns alltså två platser kvar till foto Y. Därefter är den kvarvarande platsen för foto Z bestämd. Det finns alltså 3 × 2 paket som alla innehåller just fotona X, Y och Z. (3 × 2 × 1 om man ska vara noga.)
Alltså, hur många unika julklappar kan svärmor få om vi väljer ut tre foton av fem? Jo:
Ja, svaret blir faktisk detsamma som när vi endast valde ut två foton, vilket kanske kan tyckas lite märkligt. C(5, 3) = C(5, 2). Generellt gäller att C(n, k) = C(n, (n-k)), vilket kanske blir klarare om du läser vidare.
---
Nu har vi dels sett hur notationen C(n, k) kan användas, utan att vi bryr oss om det numeriska värdet; dels har vi sett hur man faktiskt tar fram ett numeriskt värde på det som representeras. Vi skall slutligen titta på en generell definition:
I vårt exempel får vi alltså:
Den här definitionen utnyttjar en annan definition, nämligen den av fakultet (!)
I vårt exempel:
Om vi kombinerar dessa definitioner kan vi härleda vårt ursprungliga uttryck:
---
Det verkar osannolikt att någon utan kunskap om dessa metoder skulle lyckas utveckla dem på egen hand, i samband med att man griper sig an det ursprungliga problemet (middagssällskapen). Så utan förkunskaper är uppgiften helt enkelt mycket svår. Men vad det är som gör uppgiften frustrerande även med tillgång till de här metoderna?
Efter introspektion, och efter att ha pratat med en handfull matematiklärare, tror jag att det beror på två saker:
(a) Det finns ingen given lösningsmetod
(b) Man vet inte när, eller om, man är färdig
Det första skälet är intressant, på minst två sätt. Först och främst för att det exemplifierar ett problem, så som detta ofta definieras i matematikundervisning. Enligt den nya skolreformen (Gy11) ska utvecklingen av problemlösningsförmåga nu prioriteras i matematikundervisningen på grundskola och gymnasium. Jag deltar själv just nu i en fortbildning kallad Matematiklyftet, som just syftar till att lära mig (som matematiklärare) att lära mina elever att (utveckla sin förmåga att) lösa problem. Jag är inte säker på att jag kan det. Faktum är att den enda metod jag kan komma på är denna:
Jag tror nämligen inte att man kan befinna sig i en totalt obekant situation. Alternativt att om man kunde det, så skulle man inte ha något verktyg (annat än slumpen) att hantera detta. Man skulle inte kunna förbereda sig för det.
Om man delar mina tvivel på möjligheten att lösa - eller ens råka ut för - genuina "problem", enligt ovanstående definition, blir det intressant att fundera över vad man då kan mena med att det inte finns någon given lösningsmetod. Mitt svar blir att detta i så fall endast innebär att man är relativt ovan vid just den typ av problem (uppgift) som man ställs inför.
Detta innebär i sin tur att det inte finns någon väsensskillnad mellan uppgifter inom diskret matematik och uppgifter inom andra grenar av matematik som är betydligt vanligare i skolan. Det rör sig i stället om en gradskillnad, och denna förklaras helt av den utsträckning i vilken man exponeras för uppgiftstypen.
Det här med att inte veta om (när) man är färdig, det är ju något som är vanligt överallt utom i den traditionella skolmatematiken. Förmåga att hantera sådana situationer är också det ett prioriterat område för skolan - både före och efter den senaste reformen. Och det är betydligt lättare att lära ut än den mytomspunna problemlösningsförmågan. Här kan vi dessutom arbeta tillsammans över ämnesgränserna, utan problem.
Det handlar om att vara kritisk till sina egna och andras förslag, att utsätta dem för systematisk (!) prövning, att söka upp alternativ, att bjuda in och värdera kritik, m.m. Att vara skeptisk och konstruktiv samtidigt. Och social.
Att ta sig an kombinatoriska problem med friskt mod är kanske en god indikator både på hur väl skolan tillämpar, såväl som ingjuter, Kaizen.
Det första skälet är intressant, på minst två sätt. Först och främst för att det exemplifierar ett problem, så som detta ofta definieras i matematikundervisning. Enligt den nya skolreformen (Gy11) ska utvecklingen av problemlösningsförmåga nu prioriteras i matematikundervisningen på grundskola och gymnasium. Jag deltar själv just nu i en fortbildning kallad Matematiklyftet, som just syftar till att lära mig (som matematiklärare) att lära mina elever att (utveckla sin förmåga att) lösa problem. Jag är inte säker på att jag kan det. Faktum är att den enda metod jag kan komma på är denna:
Stoppa så många tekniker som möjligt i ryggsäcken, och titta på så många exempel som möjligt på hur och när dessa tekniker kan användas, så att du i en (relativt) obekant situation ger dig själv goda möjligheter att se (hitta) ett lämpligt "Heureka"-steg.
Jag tror nämligen inte att man kan befinna sig i en totalt obekant situation. Alternativt att om man kunde det, så skulle man inte ha något verktyg (annat än slumpen) att hantera detta. Man skulle inte kunna förbereda sig för det.
Om man delar mina tvivel på möjligheten att lösa - eller ens råka ut för - genuina "problem", enligt ovanstående definition, blir det intressant att fundera över vad man då kan mena med att det inte finns någon given lösningsmetod. Mitt svar blir att detta i så fall endast innebär att man är relativt ovan vid just den typ av problem (uppgift) som man ställs inför.
Detta innebär i sin tur att det inte finns någon väsensskillnad mellan uppgifter inom diskret matematik och uppgifter inom andra grenar av matematik som är betydligt vanligare i skolan. Det rör sig i stället om en gradskillnad, och denna förklaras helt av den utsträckning i vilken man exponeras för uppgiftstypen.
Det här med att inte veta om (när) man är färdig, det är ju något som är vanligt överallt utom i den traditionella skolmatematiken. Förmåga att hantera sådana situationer är också det ett prioriterat område för skolan - både före och efter den senaste reformen. Och det är betydligt lättare att lära ut än den mytomspunna problemlösningsförmågan. Här kan vi dessutom arbeta tillsammans över ämnesgränserna, utan problem.
Det handlar om att vara kritisk till sina egna och andras förslag, att utsätta dem för systematisk (!) prövning, att söka upp alternativ, att bjuda in och värdera kritik, m.m. Att vara skeptisk och konstruktiv samtidigt. Och social.
Att ta sig an kombinatoriska problem med friskt mod är kanske en god indikator både på hur väl skolan tillämpar, såväl som ingjuter, Kaizen.
Gillar du att vinna men hatar att förlora?
Jag fick nyligen ett tips om det här klippet:
På YouTube presenteras det så här:
Just det här klippet ingår kanske i samma reklamkampanj som andra liknande pinsamheter, som t.ex. mannen som inte kan acceptera att han åker ut ur en frågesport; eller kvinnan som inte är nöjd med sin låda i Bingolotto, m.fl.? De klippen har ju visats på TV nyligen, i samband med någon reklamkampanj...
Men vänta nu... är det inte lite väl bra för att vara sant? Är det fejkat? Kan det verkligen vara så? Jag vet inte vad jag ska tro:
Nu har jag bestämt mig: Det är fejk! Tror jag... Men vad tror alla andra?
Jag bestämmer mig för att våga göra bort mig. Jag tänker deklarera högt och tydligt att det här är fejk. Låt andra skratta åt mig om det visar sig vara på riktigt i alla fall. Och låt dem skratta ännu högre om det visar sig att de tvärtom tycker att det är självklart att det är fejk - hur kunde jag ens överväga något annat!
Nu gäller det att fylla på med argument till stöd för övertygelsen om att klippet är fejk (och att detta samtidigt inte är helt självklart).
Det ingår förstås i reklamkampanjen att en del tror att klippet är äkta; att vissa tvivlar, och att andra söker efter sanningen; några spekulerar, o.s.v. Smart! Det aktiverar en jädra massa psykologiska krafter, både individuellt och socialt. Om det är det reklam, ja då stannar den verkligen kvar i huvudet på folk.
Är det inte Premieobligationer det handlar om? Jag tror det. De brukar ju alltid handla om att man kan vara med även om man är en dålig förlorare - eftersom man inte kan förlora.
Nu kommer jag att tänka på ytterligare ett psykologiskt fenomen: Egentligen är skillnaden i ålder uppenbar - i efterhand (när man har bestämt sig). Men en stark vilja att tro på sådana här pinsamheter och konflikter; och att få möjligheten att sprida dem vidare, gör att man inte registrerar skillnaden (kanske t.o.m. avfärdar den).
(Usch, det här kan bli pinsamt för mig. Nu har jag utarbetat en hel teori som förklarar varför klippet är fejk utan att ens försöka ta reda på fakta. Och nu känns det nästan som om jag inte ens behöver ta reda på fakta - min teori är ju så övertygande.)
Ytterligare ett fenomen som illustreras: Reklammakarna har lagt ned så stora resurser på både produktion och spridning att det verkar osannolikt att det är fejkat. Precis som i biologin, med starka och svaga signaler: En stark signal, som man inte kan fejka (t.ex. pengar eller stora horn), tas på större allvar. Dels för att det är riskablare att inte tro på den, men också för att den i någon mening inte kan ljuga - den som signalerar har uppenbarligen stora resurser (men kanske inte just dem som behövs för att besegra dig). Den korniga bilden, däremot är en svag signal om programmets ålder: den är lätt att fejka (men bidrar förvisso till illusionen).
Reklamkampanjens strategi påminner också om en spion-thriller: Säkerhetstjänsterna är alltid noga med att desinformation ska hittas av den som ska luras, snarare än att avslöjas av "misstag".
Denna strategi utnyttjar också confirmation bias: De kopplingar du själv gör är svåra för dig att utsätta för kritisk granskning - du letar snarare efter stöd för din första, reflexmässiga tolkning.
Och hela den här texten är förstås, i sig själv, ett utsökt exempel på alla ovanstående fenomen.
Man kanske skulle försöka leta efter lite fakta i alla fall...
Jamen, titta här!
Riksgälden | Reklamfilmer
Det fanns förstås en poäng i att jag skrev allt det här utan att först söka fakta. Stark signalering, du vet...
På YouTube presenteras det så här:
Här är klippet från hyllningsprogrammet "Ett liv i sport" där Ingvar Oldsberg intervjuar svenska världsstjärnor och sportlegender. En av Patrik Sjöbergs klubbkamrater från ÖIS hävdar att han skulle ha vunnit ett distriktsmästerskap som sedermera gjort Patrik till stjärna. Otroligt pinsamt! Saboterar hela programmet!!!!Många verkar tycka att det här är riktigt roligt (själv tycker jag mest att det är hemskt). Jag har jag sett flera liknande klipp både på TV och på nätet, och de verkar vara mycket populära.
Just det här klippet ingår kanske i samma reklamkampanj som andra liknande pinsamheter, som t.ex. mannen som inte kan acceptera att han åker ut ur en frågesport; eller kvinnan som inte är nöjd med sin låda i Bingolotto, m.fl.? De klippen har ju visats på TV nyligen, i samband med någon reklamkampanj...
Men vänta nu... är det inte lite väl bra för att vara sant? Är det fejkat? Kan det verkligen vara så? Jag vet inte vad jag ska tro:
- Patrik Sjögren och Ingvar Oldsberg ser ju ut att vara i sin nuvarande ålder, men programmet ser ut att ha sänts på 90-talet.
- Är inte deltagarna lite väl märkliga? Osannolikt märkliga?
- Skulle Patrik Sjöberg verkligen kunna sitta tyst genom något sådant här?
Nu har jag bestämt mig: Det är fejk! Tror jag... Men vad tror alla andra?
Jag bestämmer mig för att våga göra bort mig. Jag tänker deklarera högt och tydligt att det här är fejk. Låt andra skratta åt mig om det visar sig vara på riktigt i alla fall. Och låt dem skratta ännu högre om det visar sig att de tvärtom tycker att det är självklart att det är fejk - hur kunde jag ens överväga något annat!
Nu gäller det att fylla på med argument till stöd för övertygelsen om att klippet är fejk (och att detta samtidigt inte är helt självklart).
Det ingår förstås i reklamkampanjen att en del tror att klippet är äkta; att vissa tvivlar, och att andra söker efter sanningen; några spekulerar, o.s.v. Smart! Det aktiverar en jädra massa psykologiska krafter, både individuellt och socialt. Om det är det reklam, ja då stannar den verkligen kvar i huvudet på folk.
Är det inte Premieobligationer det handlar om? Jag tror det. De brukar ju alltid handla om att man kan vara med även om man är en dålig förlorare - eftersom man inte kan förlora.
Nu kommer jag att tänka på ytterligare ett psykologiskt fenomen: Egentligen är skillnaden i ålder uppenbar - i efterhand (när man har bestämt sig). Men en stark vilja att tro på sådana här pinsamheter och konflikter; och att få möjligheten att sprida dem vidare, gör att man inte registrerar skillnaden (kanske t.o.m. avfärdar den).
(Usch, det här kan bli pinsamt för mig. Nu har jag utarbetat en hel teori som förklarar varför klippet är fejk utan att ens försöka ta reda på fakta. Och nu känns det nästan som om jag inte ens behöver ta reda på fakta - min teori är ju så övertygande.)
Ytterligare ett fenomen som illustreras: Reklammakarna har lagt ned så stora resurser på både produktion och spridning att det verkar osannolikt att det är fejkat. Precis som i biologin, med starka och svaga signaler: En stark signal, som man inte kan fejka (t.ex. pengar eller stora horn), tas på större allvar. Dels för att det är riskablare att inte tro på den, men också för att den i någon mening inte kan ljuga - den som signalerar har uppenbarligen stora resurser (men kanske inte just dem som behövs för att besegra dig). Den korniga bilden, däremot är en svag signal om programmets ålder: den är lätt att fejka (men bidrar förvisso till illusionen).
Reklamkampanjens strategi påminner också om en spion-thriller: Säkerhetstjänsterna är alltid noga med att desinformation ska hittas av den som ska luras, snarare än att avslöjas av "misstag".
Denna strategi utnyttjar också confirmation bias: De kopplingar du själv gör är svåra för dig att utsätta för kritisk granskning - du letar snarare efter stöd för din första, reflexmässiga tolkning.
Och hela den här texten är förstås, i sig själv, ett utsökt exempel på alla ovanstående fenomen.
Man kanske skulle försöka leta efter lite fakta i alla fall...
Jamen, titta här!
Riksgälden | Reklamfilmer
Det fanns förstås en poäng i att jag skrev allt det här utan att först söka fakta. Stark signalering, du vet...
1 juli 2013
Schackdatorernas maratonmatch: en grundsten i Dennetts kompatibilism
Nyligen utkom Daniel C. Dennetts senaste bok Intuition Pumps and Other Tools for Thinking på engelska. Nedan följer en fri och förenklad översättning av det jag anser vara bokens nyckelkapitel, kapitel 70: "A Computer Chess Marathon" (s. 384-392), i vilket Dennett anför ett slagkraftigt argument för sin version av kompatibilism, och lägger grunden till en övertygande sammanjämkning av materialism, moral och juridik (vilken han delvis genomför i de följande kapitlen).
---
Det är djävulskt svårt att tänka klart om determinism och val. Om världen är deterministisk (1), finns det då egentligen några valmöjligheter? Om en agent (2) som verkar ha en fri vilja i själva verket är deterministisk, och om den befinner sig i en deterministisk värld, måste vi då frånkänna den alla val, alla möjligheter? Låt oss undersöka frågan genom att betrakta en förenklad värld - schack - inuti en annan, konstgjord och helt deterministisk värld: en dator.
Anta att du installerar två olika schackprogram på din dator, kopplar ihop dem med ett litet övervakningsprogram, och låter dem spela mot varandra, match efter match, i en lång (kanske oändlig) följd. Kommer de att spela samma parti, om och om igen, tills du stänger av datorn? Du skulle kunna ställa in allting så, men då skulle du knappast få reda på någonting intressant om de båda programmen, A och B. Anta att A besegrar B i detta enda upprepade parti. Du skulle inte kunna dra slutsatsen att A är bättre än B, eller att A skulle besegra B i ett annat parti, och av dessa exakta upprepningar skulle du inte lära dig något om de båda programmens styrkor och svagheter. Betydligt mer intressant vore att arrangera en turnering där A och B spelar en serie olika partier. Det kan lätt ordnas. Om något av schackprogrammen använder en slumptalsgenerator (3) i sina beräkningar (om det t.ex. då och då "singlar slant" för att avgöra sitt nästa drag när inga andra skäl väger över åt något särkilt alternativ) så kommer denna att ge olika värden i olika matcher (om den inte återställs) och följaktligen kommer olika alternativ att utforskas, i en annan ordning, vilket ibland kommer att leda till att andra drag "väljs". Olika varianter av partiet kommer att spelas upp, i en serie där ingen match är den andra lik. Om du däremot startade om datorn så skulle exakt samma serie av matcher spelas upp på nytt, eftersom exakt samma slumptalsserie skulle bestämma programmens alla "slantsinglingar".
Anta nu att vi arrangerar en sådan schackturnering mellan två program, A och B, och studerar en serie av tusen matcher. Vi kommer att finna många tillförlitliga mönster. Anta att vi finner att A alltid besegrar B, i tusen olika partier. Det är ett mönster som vi skulle vilja förklara, och att påstå att "A är förutbestämt att besegra B eftersom programmen är deterministiska" skulle inte förklara någonting. Vi vill veta vad det är som gör att strukturen, metoderna och reaktionerna hos program A är överlägsna. A uppvisar en kompetens eller en styrka som B saknar, och vi måste isolera denna faktor. Förklaringen skulle kunna ligga på en låg nivå: det skulle t.ex. kunna visa sig att A och B i själva verket är samma program, identiska på programkodsnivå, men att A har kompilerats (4) effektivare och därför kan utvärdera fler drag än B på samma tid. A "tänker exakt samma tankar" som B, och B "vet" lika mycket (exakt samma saker) som A, men A tänker helt enkelt snabbare. (I verkliga turneringar används alltid en schack-klocka; om din tid tar slut innan du har gjort dina drag så förlorar du.) Men det är troligare att program A:s överlägsenhet måste förklaras på en högre nivå, där vardagliga schacköverväganden görs: representationer av brädpositioner, värderingar av olika möjliga fortsättningar, beslut om vilka möjligheter som ska utforskas djupare, o.s.v. Kanske förändrar program A det relativa värdet av sina pjäser efterhand som partiet fortgår, eller använder bättre värderingsfunktioner för brädpositioner, eller beslutar att avbryta utforskningen av vissa scenarior tidigare eller senare. Det "tänker inte samma tankar som B"; det "tänker bättre, mer sofistikerade tankar". (Typ "tänker", alltså. Det är ingen medveten person.)
Experimentet blir mer givande om samma program inte vinner varje gång. Anta att A nästan alltid besegrar B, och att A värderar olika drag enligt helt andra principer. Då skulle vi ha något än mer intressant att förklara. Och för att undersöka orsakerna till detta skulle vi behöva studera tusentals olika partier och leta efter fler mönster. Vi skulle garanterat hitta massor av dem. En del av dem skulle vara typiska för spelet schack, hur det än spelas (t.ex. att B nästan säkert förlorar de partier då det har färre torn kvar i spel), och en del skulle bero på A:s och B:s egenheter som schackspelare (t.ex. B:s tendens att flytta ut sin drottning alltför tidigt). Vi skulle hitta typiska strategiska mönster, såsom det faktum att när B:s tid håller på att ta slut söker det inte lika långt ned i spelträdet som det annars skulle ha gjort i motsvarande situation. Ja, vi skulle hitta en stor mängd förklaringsmässiga regelbundenheter, vissa undantagslösa och andra statistiska.
Alla dessa lätt igenkännliga schackdragsmönster sticker tydligt ut i den deterministiska parad som på mikro-nivå inte ser ut att innehålla några utmärkande drag. Det som ur ett perspektiv ter sig som två schackprogram inbegripna i en spännande kamp kan, genom "mikroskopet" (där vi betraktar instruktioner och data som flyter genom datorns processor) ses som en enda deterministisk automat som utför steg för steg i en enda möjlig ordning, där varje steg kan förutsägas genom granskning av det exakta tillståndet hos slumptalsgeneratorn och övriga delar av program och data. Det finns inga "verkliga" förgreningar i dess framtid; alla "val" som A och B gör är redan bestämda av det totala tillståndet hos datorn och dess minne. Ingenting, verkar det, är "möjligt" i denna värld, förutom det som faktiskt sker. Anta t.ex. att B vid tidpunkt t är nära att uppnå ett läge där vinst är garanterad efter ett visst (stort) antal drag, men att tiden tar slut och att B därför avbryter sin sökning efter det avgörande draget ett beräkningssteg för tidigt. Den där garanterade segern skulle aldrig kunna ha hänt. (Vilket vi kan bevisa, om vi tvivlar på det, genom att köra exakt samma turnering en annan dag. B:s tid skulle ta slut på exakt samma ställe, vid motsvarande tidpunkt.)
Så vad kan vi säga? Är detta verkligen en värld utan förebyggande och undvikande, utan offensiv och defensiv, utan förlorade chanser, utan verkliga subjekts anfall och försvar, i avsaknad av äkta möjligheter? Förvisso är våra schackprogram, likt insekter och fiskar, alldeles för enkla agenter för att betraktas som trovärdiga kandidater för moraliskt betydelsefull fri vilja, men determinismen i deras värld fråntar dem inte deras lika styrkor, deras olika förmågor att använda sig av de möjligheter som den erbjuder. Om vi vill förstå vad som händer i denna värld kan vi - måste vi - tala om hur deras informerade val orsakar förändringar i deras omständigheter, och om vad de kan och inte kan göra. Om vi vill frilägga de orsakssamband som förklarar de mönster vi upptäcker i de där tusen schackmatcherna så måste vi på allvar utgå från det perspektiv som beskriver en värld innehållande två agenter, A och B, vilka försöker besegra varandra i schack.
Anta att vi ställer in turneringsprogrammet så att en klocka ringer varje gång A vinner, och en vissla ljuder varje gång B vinner. Vi startar maratonmatchen och en betraktare, som inte känner till någonting om programmet, noterar att klockan ringer ganska ofta och att visslan sällan ljuder. Vad kan förklara denna regelbundenhet, undrar hon. Den regelbundenhet med vilken A besegrar B kan upptäckas och beskrivas utan att inta det intentionella förhållningssättet (5), men den kan inte förklaras. Den enda förklaringen - rätt förklaring - kan vara att A:s "föreställning" om vad B kommer att göra om... är bättre än B:s "föreställning" om vad A kommer att göra om... I sådana fall är det nödvändigt att inta det intentionella förhållningssättet för att hitta förklaringen.
Allt väl, så långt. Men alla dessa "beslut" och "val" verkar bara vara... typ beslut och val. Det verkar som om de saknar någonting som verkliga val har: "kunde ha gjort något annat". Men låt oss titta närmare på ett specifikt exempel, eftersom allt inte är vad det verkar vara. Det underlättar om vi tar med ett tredje schackspelarprogram, C, i vår turnering. Och låt oss anta att C är bättre än A och B och nästan alltid besegrar dem. Vi antar vidare att de första tolv dragen i ett par av dessa matcher är exakt desamma och att C vinner båda och besegrar både A och B, fast längs två olika vägar efter de första tolv dragen. De experter som i efterhand analyserar partierna klurar ut att om A eller B som sina tolfte (och sista gemensamma) drag hade gjort en rockad så hade C troligen förlorat. En rockad i tolfte draget var nyckeln till vinst, och det missade både A och B.
Personen som har skapat program A rycker på axlarna och säger: "Tja, mitt program, A, kunde ha gjort en rockad", och personen som har skapat program B svarar "Det kunde mitt program, B, också ha gjort". Men skaparen av program A har rätt medan skaparen av program B har fel! Hur kan det vara så? Turneringsprogrammet T är deterministiskt, och om vi kör matcherna igen, från exakt samma utgångstillstånd, kommer vare sig A eller B att göra en rockad. Lurar inte skaparen av program A sig själv? Inte nödvändigtvis. Vad är det vi försöker ta reda på när vi frågar om A hade kunnat agera annorlunda? Att titta på exakt samma parti, om och om igen, ger ingen information. Men att titta på liknande fall är däremot upplysande. Om vi märker att A i många andra liknande situationer i andra partier faktiskt fortsätter sin utvärdering lite längre, upptäcker värdet av en rockad och genomför den, då kan vi ställa oss bakom programskaparens övertygelse att A kunde ha gjort en rockad.
Vi skulle kunna upptäcka att det hade räckt att skifta en enda bit (6) i slumptalsgeneratorn för att A skulle ha gjort en rockad. Anta att A:s skapare gräver djupt i körningen av programmet och kan visa att A, i det här fallet, avbröt sin utvärdering ett enda beräkningssteg för tidigt. (Alla schackprogram, oavsett hur bra de är, måste avbryta sin sökning efter det bästa möjliga draget godtyckligt vid någon tidpunkt.) A övervägde en rockad, och hade påbörjat sin analys av det förväntade resultatet, men eftersom tiden höll på att ta slut vände den sig till slumptalsgeneratorn, "singlade slant" och nöjde sig med det bästa drag som den hittills hade funnit - och det var inte en rockad. Om slumptalet hade blivit en etta i stället för en nolla så hade A fortsatt sin analys ytterligare några steg, och gjort en rockad. "Skifta bara en enda bit i slumptalet så vinner A!" säger skaparen. Vi skulle säga att i det här fallet var A:s uteblivna rockad oflax, otur med slumptalsgeneratorn.
När vi vänder oss till skaparen av program B får vi ingen motsvarande redogörelse som stöd för påståendet att B skulle ha kunnat göra en rockad under de aktuella omständigheterna. Det stämmer att B "vet" att en rockad är möjlig i denna situation, och kanske också att det som hastigast "övervägde" rockad, men B var inte i närheten av att välja rockad vid det här tillfället. Rockaden var ett "djupt" drag, den sorts drag som åtföljs av ett "(!)" i tidningarnas schackkolumner, och långt bortom B:s begränsade analyskapacitet. Här har vi alltså en helt deterministisk värld - program T - i vilken A kunde ha gjort en rockad, men B inte kunde ha gjort det. Skillnaden mellan A och B är verklig och har förklaringskraft, en skillnad i kompetens eller förmåga. Ett sätt att uttrycka det är uppenbart motsägelsefullt:
Vad skulle rimligen kunna rättfärdiga detta sätt att beskriva situationen? Helt enkelt detta: om vi betraktar A avskild från dess omedelbara omgivning - vilken innefattar slumptalsgeneratorn - då är A:s val att göra en rockad eller inte obestämt. Det beror på något som strikt talat ligger utanför systemet. Givet det sätt på vilket resten av världen var organiserad vid tidpunkt t var en rockad inte möjlig för A, men det är "inte A:s fel". B, å andra sidan, skulle inte ha kunnat göra en rockad; det låg inte i B:s natur att göra en rockad. Att föreställa sig B göra en rockad skulle kräva alltför många modifikationer av den föreliggande situationen.
Det här är en användbar upptäckt: en distinktion mellan vad A och B "kunde göra" som inte är beroende av indeterminism. Även i en deterministisk värld kan vi se att A kan göra vissa slags saker som B inte kan göra, och denna skillnad är en del av förklaringen till varför A besegrar B. Det faktum att determinismen i den här världen innebär att A och B bara kan göra det som de faktiskt gör vid det aktuella tillfället (och skulle göra igen och igen om exakt samma omständigheter upprepades) är helt enkelt inte intressant, och inte relevant för förklaringen vi får till den helt objektiva och tydliga regelbundenheten: A besegrar B.
Ett schackprogram är inte en moralisk agent, och det är inte moraliskt ansvarigt för de val det gör - dess värld är helt amoralisk, och att bryta mot någon av schackreglerna är helt enkelt otänkbart för ett schackprogram, och kräver därför inga straff för överträdelser. Men som vi just har sett, kan vi även i datorschackets enkla och deterministiska värld peka på en verklig och viktig skillnad mellan A och B. Ibland, när A gör något dumt eller smart, kan vi säga "A kunde ha gjort något annat, men B kunde inte ha gjort något annat". Om du tänker att det måste vara ett misstag, för att "vare sig A eller B kunde någonsin ha gjort något annat eftersom världen är deterministisk", så är det du som gör misstaget.
A och B skiljer sig åt i schackspelsförmåga, och "kunde ha gjort något annat" fångar snyggt in en del av den skillnaden, som vi precis har sett. Hur är det med moralisk förmåga? När folk säger att vissa människor som gör dumma saker "kunde ha agerat annorlunda" och använder detta som ursäkt för att inte förlåta dem, och samtidigt menar att andra människor i liknande situationer inte kunde ha agerat annorlunda, begår inte heller de något misstag - och detta oberoende av huruvida världen är deterministisk eller inte. De framhåller en verklig skillnad i moralisk kompetens som inte beror på vare sig determinism eller indeterminism, och som kan ligga till grund för en skillnad i hur vi reagerar.
För att se detta tydligare kan du tänka dig att det är du som har skapat program B. Du vill veta om du har upptäckt en svaghet i B. Här har vi ett parti där en utebliven rockad kostade segern; kunde då B ha gjort en rockad? Om allt som krävdes för det var att skifta en enstaka bit i slumptalsgeneratorn, ja, då kanske inga förbättringar är påkallade. I liknande situationer händer det alltsomoftast att B gör en rockad, och bättre än så kan det kanske inte bli. Alla program måste använda slumptal då och då ("singla slant") för att avsluta sökningar och komma vidare, och därför kommer det alltid att uppstå tillfällen där sökningen avbryts precis innan en upptäckt, på grund av en slantsingling. Och lägg märke till att det inte hjälper att använda en kvant-slumptalsgenerator, t.ex. en Geiger-mätare som spyr ur sig bitar baserade på sub-atomära partiklars obestämda banor. Fundera på vad vi då skulle säga om B i det fall då B inte gör en rockad på grund av en enstaka nolla där det kunde ha varit en etta. Om kvant-slumpgeneratorn ger ifrån sig en nolla så gör B en rockad; om den ger ifrån sig en etta så gör B inte en rockad. "B kunde ha gjort en rockad" säger någon när ettan dyker upp. Ja, men B är inte friare för det. I en följd av partier där sådana här situationer förekommer, kommer B att göra en rockad i hälften av fallen, och inte göra en rockad i den andra hälften, oavsett om slumptalsgeneratorn är "äkta" eller "pseudo". Filosofen David Wiggins skrev en gång om determinismens "kosmiska orättvisa" men vår intuitionspump visar att indeterminismen är lika "kosmiskt orättvis". B är "utlämnad åt" sin slumptalsgenerator eller sin pseudo-slumptalsgenerator (Det är förstås A också; det är vi allihop.) Det finns ingen anledning att föredra den äkta slumptalsgeneratorn - om du inte planerar att spela schack mot en allvetande Gud, förstås, som kan skärskåda din pseudo-slumptalsgenerator och planera därefter!
Så, vi söker fortfarande efter en anledning att önska indeterminism. Kanske kan vi få all den fria vilja som är värd att önska sig utan att indeterminism spelar någon roll. Här är ett annat möjligt skäl:
Näpp. Ändra framtiden från vad till vad? Från det den skulle ha blivit till det den kommer att bli? Du kan inte ändra framtiden mer än vad du kan ändra det förflutna. Begreppet är oklart. Så:
Varför verkar det som om vi vill ändra framtiden? Därför att vi vill kunna förutse olyckor och göra något för att dessa olyckor inte ska inträffa. Och det kan vi göra, oberoende av indeterminism. Om någon kastar en tegelsten mot dig och du ser den och duckar så kan du undvika att bli träffad av tegelstenen. Bra för dig. Skulle kollisionen ha ägt rum? I en mening, ja, eftersom stenen tydligt var på väg mot ditt huvud, men eftersom du såg den (vilket orsakades av ljuset som studsade från den in i dina ögon där din din hjärna beräknade risken, vilket fick den att vidta handling), undvek du den. Om du hade velat undvika att undvika den (om något skäl till varför det faktiskt skulle vara bättre för dig att låta den träffa dig hade föresvävat dig), hade du förstås kunnat göra just det. En observatör skulle kanske inte kunna avgöra, förrän i sista ögonblicket, om du skulle bli träffad eller inte. Och om han hade slagit vad om att du skulle ducka så hade han förlorat. Vi är tillbaks till vårt skäl att vilja vara oförutsägbara, vilket inte kräver indeterminism.
Vad åstadkommer den här intuitionspumpen? Den tar den välbekanta frasen "kunde ha agerat annorlunda" och visar att den, i motsats till den utbredda men ogenomtänkta uppfattningen, i en viktig mening inte är beroende av indeterminism. Om det finns en betydelse av "kunde ha agerat annorlunda" som är både inkompatibel med determinism och moraliskt viktig - inte bara en metafysisk kuriositet - så återstår det att visas, och bevisbördan ligger på dem som tror att det är så. Ytterligare en "självklarhet" avslöjad som inte fullt så självklar trots allt.
---
1. I princip förutbestämd; möjlig att förutse.
2. Någon eller något som verkar i världen på ett till synes målinriktat sätt.
3. Egentligen en pseudo-slumptalsgenerator, vars värden i princip kan förutsägas.
4. En kompilator översätter ett program skrivet av en människa till instruktioner som en dator kan följa.
5. Att betrakta något (någon) som målinriktat, rationellt; som om det tror och önskar saker.
6. Den minsta enheten i en dators minne, vilken innehåller antingen 1 eller 0.
---
Det är djävulskt svårt att tänka klart om determinism och val. Om världen är deterministisk (1), finns det då egentligen några valmöjligheter? Om en agent (2) som verkar ha en fri vilja i själva verket är deterministisk, och om den befinner sig i en deterministisk värld, måste vi då frånkänna den alla val, alla möjligheter? Låt oss undersöka frågan genom att betrakta en förenklad värld - schack - inuti en annan, konstgjord och helt deterministisk värld: en dator.
Anta att du installerar två olika schackprogram på din dator, kopplar ihop dem med ett litet övervakningsprogram, och låter dem spela mot varandra, match efter match, i en lång (kanske oändlig) följd. Kommer de att spela samma parti, om och om igen, tills du stänger av datorn? Du skulle kunna ställa in allting så, men då skulle du knappast få reda på någonting intressant om de båda programmen, A och B. Anta att A besegrar B i detta enda upprepade parti. Du skulle inte kunna dra slutsatsen att A är bättre än B, eller att A skulle besegra B i ett annat parti, och av dessa exakta upprepningar skulle du inte lära dig något om de båda programmens styrkor och svagheter. Betydligt mer intressant vore att arrangera en turnering där A och B spelar en serie olika partier. Det kan lätt ordnas. Om något av schackprogrammen använder en slumptalsgenerator (3) i sina beräkningar (om det t.ex. då och då "singlar slant" för att avgöra sitt nästa drag när inga andra skäl väger över åt något särkilt alternativ) så kommer denna att ge olika värden i olika matcher (om den inte återställs) och följaktligen kommer olika alternativ att utforskas, i en annan ordning, vilket ibland kommer att leda till att andra drag "väljs". Olika varianter av partiet kommer att spelas upp, i en serie där ingen match är den andra lik. Om du däremot startade om datorn så skulle exakt samma serie av matcher spelas upp på nytt, eftersom exakt samma slumptalsserie skulle bestämma programmens alla "slantsinglingar".
Anta nu att vi arrangerar en sådan schackturnering mellan två program, A och B, och studerar en serie av tusen matcher. Vi kommer att finna många tillförlitliga mönster. Anta att vi finner att A alltid besegrar B, i tusen olika partier. Det är ett mönster som vi skulle vilja förklara, och att påstå att "A är förutbestämt att besegra B eftersom programmen är deterministiska" skulle inte förklara någonting. Vi vill veta vad det är som gör att strukturen, metoderna och reaktionerna hos program A är överlägsna. A uppvisar en kompetens eller en styrka som B saknar, och vi måste isolera denna faktor. Förklaringen skulle kunna ligga på en låg nivå: det skulle t.ex. kunna visa sig att A och B i själva verket är samma program, identiska på programkodsnivå, men att A har kompilerats (4) effektivare och därför kan utvärdera fler drag än B på samma tid. A "tänker exakt samma tankar" som B, och B "vet" lika mycket (exakt samma saker) som A, men A tänker helt enkelt snabbare. (I verkliga turneringar används alltid en schack-klocka; om din tid tar slut innan du har gjort dina drag så förlorar du.) Men det är troligare att program A:s överlägsenhet måste förklaras på en högre nivå, där vardagliga schacköverväganden görs: representationer av brädpositioner, värderingar av olika möjliga fortsättningar, beslut om vilka möjligheter som ska utforskas djupare, o.s.v. Kanske förändrar program A det relativa värdet av sina pjäser efterhand som partiet fortgår, eller använder bättre värderingsfunktioner för brädpositioner, eller beslutar att avbryta utforskningen av vissa scenarior tidigare eller senare. Det "tänker inte samma tankar som B"; det "tänker bättre, mer sofistikerade tankar". (Typ "tänker", alltså. Det är ingen medveten person.)
Experimentet blir mer givande om samma program inte vinner varje gång. Anta att A nästan alltid besegrar B, och att A värderar olika drag enligt helt andra principer. Då skulle vi ha något än mer intressant att förklara. Och för att undersöka orsakerna till detta skulle vi behöva studera tusentals olika partier och leta efter fler mönster. Vi skulle garanterat hitta massor av dem. En del av dem skulle vara typiska för spelet schack, hur det än spelas (t.ex. att B nästan säkert förlorar de partier då det har färre torn kvar i spel), och en del skulle bero på A:s och B:s egenheter som schackspelare (t.ex. B:s tendens att flytta ut sin drottning alltför tidigt). Vi skulle hitta typiska strategiska mönster, såsom det faktum att när B:s tid håller på att ta slut söker det inte lika långt ned i spelträdet som det annars skulle ha gjort i motsvarande situation. Ja, vi skulle hitta en stor mängd förklaringsmässiga regelbundenheter, vissa undantagslösa och andra statistiska.
Alla dessa lätt igenkännliga schackdragsmönster sticker tydligt ut i den deterministiska parad som på mikro-nivå inte ser ut att innehålla några utmärkande drag. Det som ur ett perspektiv ter sig som två schackprogram inbegripna i en spännande kamp kan, genom "mikroskopet" (där vi betraktar instruktioner och data som flyter genom datorns processor) ses som en enda deterministisk automat som utför steg för steg i en enda möjlig ordning, där varje steg kan förutsägas genom granskning av det exakta tillståndet hos slumptalsgeneratorn och övriga delar av program och data. Det finns inga "verkliga" förgreningar i dess framtid; alla "val" som A och B gör är redan bestämda av det totala tillståndet hos datorn och dess minne. Ingenting, verkar det, är "möjligt" i denna värld, förutom det som faktiskt sker. Anta t.ex. att B vid tidpunkt t är nära att uppnå ett läge där vinst är garanterad efter ett visst (stort) antal drag, men att tiden tar slut och att B därför avbryter sin sökning efter det avgörande draget ett beräkningssteg för tidigt. Den där garanterade segern skulle aldrig kunna ha hänt. (Vilket vi kan bevisa, om vi tvivlar på det, genom att köra exakt samma turnering en annan dag. B:s tid skulle ta slut på exakt samma ställe, vid motsvarande tidpunkt.)
Så vad kan vi säga? Är detta verkligen en värld utan förebyggande och undvikande, utan offensiv och defensiv, utan förlorade chanser, utan verkliga subjekts anfall och försvar, i avsaknad av äkta möjligheter? Förvisso är våra schackprogram, likt insekter och fiskar, alldeles för enkla agenter för att betraktas som trovärdiga kandidater för moraliskt betydelsefull fri vilja, men determinismen i deras värld fråntar dem inte deras lika styrkor, deras olika förmågor att använda sig av de möjligheter som den erbjuder. Om vi vill förstå vad som händer i denna värld kan vi - måste vi - tala om hur deras informerade val orsakar förändringar i deras omständigheter, och om vad de kan och inte kan göra. Om vi vill frilägga de orsakssamband som förklarar de mönster vi upptäcker i de där tusen schackmatcherna så måste vi på allvar utgå från det perspektiv som beskriver en värld innehållande två agenter, A och B, vilka försöker besegra varandra i schack.
Anta att vi ställer in turneringsprogrammet så att en klocka ringer varje gång A vinner, och en vissla ljuder varje gång B vinner. Vi startar maratonmatchen och en betraktare, som inte känner till någonting om programmet, noterar att klockan ringer ganska ofta och att visslan sällan ljuder. Vad kan förklara denna regelbundenhet, undrar hon. Den regelbundenhet med vilken A besegrar B kan upptäckas och beskrivas utan att inta det intentionella förhållningssättet (5), men den kan inte förklaras. Den enda förklaringen - rätt förklaring - kan vara att A:s "föreställning" om vad B kommer att göra om... är bättre än B:s "föreställning" om vad A kommer att göra om... I sådana fall är det nödvändigt att inta det intentionella förhållningssättet för att hitta förklaringen.
Allt väl, så långt. Men alla dessa "beslut" och "val" verkar bara vara... typ beslut och val. Det verkar som om de saknar någonting som verkliga val har: "kunde ha gjort något annat". Men låt oss titta närmare på ett specifikt exempel, eftersom allt inte är vad det verkar vara. Det underlättar om vi tar med ett tredje schackspelarprogram, C, i vår turnering. Och låt oss anta att C är bättre än A och B och nästan alltid besegrar dem. Vi antar vidare att de första tolv dragen i ett par av dessa matcher är exakt desamma och att C vinner båda och besegrar både A och B, fast längs två olika vägar efter de första tolv dragen. De experter som i efterhand analyserar partierna klurar ut att om A eller B som sina tolfte (och sista gemensamma) drag hade gjort en rockad så hade C troligen förlorat. En rockad i tolfte draget var nyckeln till vinst, och det missade både A och B.
Personen som har skapat program A rycker på axlarna och säger: "Tja, mitt program, A, kunde ha gjort en rockad", och personen som har skapat program B svarar "Det kunde mitt program, B, också ha gjort". Men skaparen av program A har rätt medan skaparen av program B har fel! Hur kan det vara så? Turneringsprogrammet T är deterministiskt, och om vi kör matcherna igen, från exakt samma utgångstillstånd, kommer vare sig A eller B att göra en rockad. Lurar inte skaparen av program A sig själv? Inte nödvändigtvis. Vad är det vi försöker ta reda på när vi frågar om A hade kunnat agera annorlunda? Att titta på exakt samma parti, om och om igen, ger ingen information. Men att titta på liknande fall är däremot upplysande. Om vi märker att A i många andra liknande situationer i andra partier faktiskt fortsätter sin utvärdering lite längre, upptäcker värdet av en rockad och genomför den, då kan vi ställa oss bakom programskaparens övertygelse att A kunde ha gjort en rockad.
Vi skulle kunna upptäcka att det hade räckt att skifta en enda bit (6) i slumptalsgeneratorn för att A skulle ha gjort en rockad. Anta att A:s skapare gräver djupt i körningen av programmet och kan visa att A, i det här fallet, avbröt sin utvärdering ett enda beräkningssteg för tidigt. (Alla schackprogram, oavsett hur bra de är, måste avbryta sin sökning efter det bästa möjliga draget godtyckligt vid någon tidpunkt.) A övervägde en rockad, och hade påbörjat sin analys av det förväntade resultatet, men eftersom tiden höll på att ta slut vände den sig till slumptalsgeneratorn, "singlade slant" och nöjde sig med det bästa drag som den hittills hade funnit - och det var inte en rockad. Om slumptalet hade blivit en etta i stället för en nolla så hade A fortsatt sin analys ytterligare några steg, och gjort en rockad. "Skifta bara en enda bit i slumptalet så vinner A!" säger skaparen. Vi skulle säga att i det här fallet var A:s uteblivna rockad oflax, otur med slumptalsgeneratorn.
När vi vänder oss till skaparen av program B får vi ingen motsvarande redogörelse som stöd för påståendet att B skulle ha kunnat göra en rockad under de aktuella omständigheterna. Det stämmer att B "vet" att en rockad är möjlig i denna situation, och kanske också att det som hastigast "övervägde" rockad, men B var inte i närheten av att välja rockad vid det här tillfället. Rockaden var ett "djupt" drag, den sorts drag som åtföljs av ett "(!)" i tidningarnas schackkolumner, och långt bortom B:s begränsade analyskapacitet. Här har vi alltså en helt deterministisk värld - program T - i vilken A kunde ha gjort en rockad, men B inte kunde ha gjort det. Skillnaden mellan A och B är verklig och har förklaringskraft, en skillnad i kompetens eller förmåga. Ett sätt att uttrycka det är uppenbart motsägelsefullt:
A kunde ha gjort en rockad vid tidpunkt t men världen kunde inte ha innehållit en rockad vid tidpunkt t.
Vad skulle rimligen kunna rättfärdiga detta sätt att beskriva situationen? Helt enkelt detta: om vi betraktar A avskild från dess omedelbara omgivning - vilken innefattar slumptalsgeneratorn - då är A:s val att göra en rockad eller inte obestämt. Det beror på något som strikt talat ligger utanför systemet. Givet det sätt på vilket resten av världen var organiserad vid tidpunkt t var en rockad inte möjlig för A, men det är "inte A:s fel". B, å andra sidan, skulle inte ha kunnat göra en rockad; det låg inte i B:s natur att göra en rockad. Att föreställa sig B göra en rockad skulle kräva alltför många modifikationer av den föreliggande situationen.
Det här är en användbar upptäckt: en distinktion mellan vad A och B "kunde göra" som inte är beroende av indeterminism. Även i en deterministisk värld kan vi se att A kan göra vissa slags saker som B inte kan göra, och denna skillnad är en del av förklaringen till varför A besegrar B. Det faktum att determinismen i den här världen innebär att A och B bara kan göra det som de faktiskt gör vid det aktuella tillfället (och skulle göra igen och igen om exakt samma omständigheter upprepades) är helt enkelt inte intressant, och inte relevant för förklaringen vi får till den helt objektiva och tydliga regelbundenheten: A besegrar B.
Ett schackprogram är inte en moralisk agent, och det är inte moraliskt ansvarigt för de val det gör - dess värld är helt amoralisk, och att bryta mot någon av schackreglerna är helt enkelt otänkbart för ett schackprogram, och kräver därför inga straff för överträdelser. Men som vi just har sett, kan vi även i datorschackets enkla och deterministiska värld peka på en verklig och viktig skillnad mellan A och B. Ibland, när A gör något dumt eller smart, kan vi säga "A kunde ha gjort något annat, men B kunde inte ha gjort något annat". Om du tänker att det måste vara ett misstag, för att "vare sig A eller B kunde någonsin ha gjort något annat eftersom världen är deterministisk", så är det du som gör misstaget.
A och B skiljer sig åt i schackspelsförmåga, och "kunde ha gjort något annat" fångar snyggt in en del av den skillnaden, som vi precis har sett. Hur är det med moralisk förmåga? När folk säger att vissa människor som gör dumma saker "kunde ha agerat annorlunda" och använder detta som ursäkt för att inte förlåta dem, och samtidigt menar att andra människor i liknande situationer inte kunde ha agerat annorlunda, begår inte heller de något misstag - och detta oberoende av huruvida världen är deterministisk eller inte. De framhåller en verklig skillnad i moralisk kompetens som inte beror på vare sig determinism eller indeterminism, och som kan ligga till grund för en skillnad i hur vi reagerar.
För att se detta tydligare kan du tänka dig att det är du som har skapat program B. Du vill veta om du har upptäckt en svaghet i B. Här har vi ett parti där en utebliven rockad kostade segern; kunde då B ha gjort en rockad? Om allt som krävdes för det var att skifta en enstaka bit i slumptalsgeneratorn, ja, då kanske inga förbättringar är påkallade. I liknande situationer händer det alltsomoftast att B gör en rockad, och bättre än så kan det kanske inte bli. Alla program måste använda slumptal då och då ("singla slant") för att avsluta sökningar och komma vidare, och därför kommer det alltid att uppstå tillfällen där sökningen avbryts precis innan en upptäckt, på grund av en slantsingling. Och lägg märke till att det inte hjälper att använda en kvant-slumptalsgenerator, t.ex. en Geiger-mätare som spyr ur sig bitar baserade på sub-atomära partiklars obestämda banor. Fundera på vad vi då skulle säga om B i det fall då B inte gör en rockad på grund av en enstaka nolla där det kunde ha varit en etta. Om kvant-slumpgeneratorn ger ifrån sig en nolla så gör B en rockad; om den ger ifrån sig en etta så gör B inte en rockad. "B kunde ha gjort en rockad" säger någon när ettan dyker upp. Ja, men B är inte friare för det. I en följd av partier där sådana här situationer förekommer, kommer B att göra en rockad i hälften av fallen, och inte göra en rockad i den andra hälften, oavsett om slumptalsgeneratorn är "äkta" eller "pseudo". Filosofen David Wiggins skrev en gång om determinismens "kosmiska orättvisa" men vår intuitionspump visar att indeterminismen är lika "kosmiskt orättvis". B är "utlämnad åt" sin slumptalsgenerator eller sin pseudo-slumptalsgenerator (Det är förstås A också; det är vi allihop.) Det finns ingen anledning att föredra den äkta slumptalsgeneratorn - om du inte planerar att spela schack mot en allvetande Gud, förstås, som kan skärskåda din pseudo-slumptalsgenerator och planera därefter!
Så, vi söker fortfarande efter en anledning att önska indeterminism. Kanske kan vi få all den fria vilja som är värd att önska sig utan att indeterminism spelar någon roll. Här är ett annat möjligt skäl:
Jag kan inte ändra det förflutna, men om världen är indeterministisk kan jag ändra framtiden!
Näpp. Ändra framtiden från vad till vad? Från det den skulle ha blivit till det den kommer att bli? Du kan inte ändra framtiden mer än vad du kan ändra det förflutna. Begreppet är oklart. Så:
Om världen är deterministisk så kan jag inte ändra framtiden, och om världen inte är deterministisk så kan jag inte ändra framtiden. Av detta följer att jag inte kan ändra framtiden.
Varför verkar det som om vi vill ändra framtiden? Därför att vi vill kunna förutse olyckor och göra något för att dessa olyckor inte ska inträffa. Och det kan vi göra, oberoende av indeterminism. Om någon kastar en tegelsten mot dig och du ser den och duckar så kan du undvika att bli träffad av tegelstenen. Bra för dig. Skulle kollisionen ha ägt rum? I en mening, ja, eftersom stenen tydligt var på väg mot ditt huvud, men eftersom du såg den (vilket orsakades av ljuset som studsade från den in i dina ögon där din din hjärna beräknade risken, vilket fick den att vidta handling), undvek du den. Om du hade velat undvika att undvika den (om något skäl till varför det faktiskt skulle vara bättre för dig att låta den träffa dig hade föresvävat dig), hade du förstås kunnat göra just det. En observatör skulle kanske inte kunna avgöra, förrän i sista ögonblicket, om du skulle bli träffad eller inte. Och om han hade slagit vad om att du skulle ducka så hade han förlorat. Vi är tillbaks till vårt skäl att vilja vara oförutsägbara, vilket inte kräver indeterminism.
Vad åstadkommer den här intuitionspumpen? Den tar den välbekanta frasen "kunde ha agerat annorlunda" och visar att den, i motsats till den utbredda men ogenomtänkta uppfattningen, i en viktig mening inte är beroende av indeterminism. Om det finns en betydelse av "kunde ha agerat annorlunda" som är både inkompatibel med determinism och moraliskt viktig - inte bara en metafysisk kuriositet - så återstår det att visas, och bevisbördan ligger på dem som tror att det är så. Ytterligare en "självklarhet" avslöjad som inte fullt så självklar trots allt.
---
1. I princip förutbestämd; möjlig att förutse.
2. Någon eller något som verkar i världen på ett till synes målinriktat sätt.
3. Egentligen en pseudo-slumptalsgenerator, vars värden i princip kan förutsägas.
4. En kompilator översätter ett program skrivet av en människa till instruktioner som en dator kan följa.
5. Att betrakta något (någon) som målinriktat, rationellt; som om det tror och önskar saker.
6. Den minsta enheten i en dators minne, vilken innehåller antingen 1 eller 0.
30 juni 2013
Sweet Tooth: varning för tandröta
Jag törstade efter en form av naiv realism. Jag blev särskilt uppmärksam, jag sträckte fram mitt läsarhuvud, så snart det nämndes en Londongata som jag kände till, eller en klänningsmodell, en verklig offentlig person, till och med ett bilmärke. Då, trodde jag, hade jag en måttstock, jag kunde bedöma skrivandets kvalitet utifrån dess exakthet, utifrån hur väl det gick i linje med mina egna intryck, eller förstärkte dem. [...] Jag var inte imponerad av de där författarna (de var utspridda över Sydamerika och Nordamerika) som nästlade sig in på sina egna sidor som en del av persongalleriet, fast beslutna att påminna den arma läsaren om att samtliga gestalter och till och med de själva var rena fantasifoster och att det fanns en skillnad mellan fiktion och liv. Eller, tvärtom, hävdade att att livet hur som helst var en fiktion. Endast författare, tänkte jag, löpte någonsin risken att blanda ihop dem. Jag var en boren empiriker. Jag trodde att författare fick betalt för att låtsas och att de, där det var lämpligt, borde använda sig av den verkliga världen, den som vi alla hade gemensamt, för att skänka trovärdighet åt allt de hade hittat på. Alltså inget köpslående om begränsningarna för deras konst, ingen trolöshet mot läsaren genom att i förklädnad tyckas gå av och an över det imaginäras gränser. [...]
(s. 78)
John Mullan beskriver i Guardian hur McEwan lyckas lura både sin läsare och sin protagonist. Efter en mycket vaksam läsning känner jag mig inte särskilt lurad. Jag misstänker däremot att McEwan driver med sig själv. Helt klart driver han i varje fall med läsare som jag. Och kanske med hela den postmodernistiska genren? Kanske säger han: "Visst, trolleritrick kan vara kul. Men någon jävla ordning får det vara." Eller kanske snarare: "Hör du, Auster - så här ska det gå till".
[...] Inte förrän på sista sidan upptäckte jag att berättelsen jag läste i själva verket var den som kvinnan höll på att skriva. Apan existerar inte, den är en gengångare, ett foster av hennes enerverande fantasi. Nej. Och åter nej. Inte detta. Bortom den krystade och löjliga frågan om sex över artgränserna misstrodde jag instinktivt den här sortens litterära konstgrepp. Jag ville känna marken under mina fötter. Det fanns, enligt min åsikt, en oskriven överenskommelse med läsaren som författaren måste följa. Inget enda inslag i en fantasivärld och ingen av dess gestalter skulle tillåtas att lösa upp sig på grund av en nyck från författaren. Det påhittade måste vara lika gediget och lika förenligt med sina egna förutsättningar som det verkliga. Det var en överenskommelse grundad på ömsesidig tillit.
(s. 216)
Men boken är mycket rikare och mer mångfacetterad än så. Utöver den litterära experimentlådan, utöver 70-talsbeskrivningen, och utöver det jag karakteriserat som en insiktsfull tablå av "psykologiska invarianter guppande i samhällskulturella dyningar med decennielånga våglängder" - Om jag bara i detta sökande hade mött en enda uppenbart ondskefull människa - finns här också en diskussion av relationen mellan konst, humaniora och (natur)vetenskap. (Det är inte utan orsak som McEwan tillhör nätverket Edge. Boken är för övrigt tillägnad Christopher Hitchens.) Och man måste bara älska de två kapitel där sannolikhetsproblemet uppkallat efter Monty Hall (!) studsar runt i dessa olika världar och bland annat får Författaren att drabbas av yrsel och illamående, och Förläggaren att drabbas av leda.
Vad den definitivt inte är - i varje fall inte till den grad som de enda två citaten på pocketutgåvans pärmar vill göra gällande - är en "stilsäker agentroman" (Sundsvalls tidning) eller en "spionroman" (Expressen). Det vore en stor, om än osannolik, tragedi om recensenter och förläggare faktiskt uppfattade den så. Men minst lika tragiskt är att genuin kvalitet alltså aktivt måste döljas på en marknad där vinning står att göras endast med lättsmält godis. Som att kränga Bachs cellosviter som "perfekt avslappning för lata dagar på stranden".
(Redan efter de första sidorna bad jag min fru att läsa boken efter mig. Jag ville att hon skulle ta ställning till hur väl McEwan lyckas inta en kvinnas perspektiv. Det var något där som skavde... något om sex, relationer, könsroller... men jag ville inte tro att McEwan skulle göra mig besviken. --- Besviken blev jag däremot i efterhand på de recensenter som framhöll just detta som en brist.)
Sidhänvisningarna och citaten gäller pocketutgåvan av [Uppdrag] Sweet Tooth av Ian McEwan, översatt till svenska av Maria Ekman och utgiven av Brombergs 2012.
Prenumerera på:
Inlägg (Atom)