En riksdagsledamot har 10 stycken vänner i riksdagen. Hon vill bjuda in fyra av dessa vänner till en gemensam middag, men vet också att hon inte kan bjuda in de båda vännerna Amanda och Benjamin samtidigt, eftersom dessa inte kommer överens med varandra.
På hur många sätt kan hon välja fyra av de tio vännerna, utan att hon väljer både Amanda och Benjamin?
Den här uppgiften är hämtad från Mattekampen 2013, ett initiativ av Mattecentrum.
Uppgiften är ett exempel på kombinatorik, som i sin tur är en gren av diskret matematik.
Den är svår - ovanligt svår för att ingå i ett test för riksdagspolitiker. Ja, svår även för de flesta som precis har gått ut gymnasiet. Eller högskolan, för den delen. Svår t.o.m. för de - få - som faktiskt läser, eller har läst, just diskret matematik (på gymnasiet).
Mitt syfte med den här texten är att särskilt lyfta fram en av orsakerna till varför uppgiften uppfattas som svår (det finns flera).
En kollega och jag roade oss med att diskutera uppgiften över en öl en fredag eftermiddag efter jobbet. Och redan här finns flera ledtrådar: Vissa människor tycker uppenbarligen att sådana här problem är roliga! Samtidigt - ja, samtidigt - kan de upplevas som krävande, skrämmande och frustrerande. För många människor, och detta inkluderar matematiker och matematiklärare - är de enbart frustrerande.
För någon som är van vid att lösa den här typen av problem är mycket givet på förhand: Man vet vilka metoder som ska användas, och man vet dessutom hur och varför dessa metoder fungerar. Trots detta är vägen till en lösning inte självklar. Värre än så: huruvida en färdig lösning faktiskt är korrekt är också ofta långt ifrån självklart. Så mycket värre för någon som tvingas resonera sig fram till en lösning utan tillgång till färdiga metoder.
Här följer några exempel på lösningar, utförda med hjälp av standardmetoder.
A. En ska bort
Om man först plockar bort Amanda, på hur många sätt kan man då välja fyra personer av de nio som återstår? Låt oss kalla svaret på den frågan för C(9, 4). Ingen av dessa sällskap innehåller både Amanda och Benjamin, eftersom Amanda inte är med i urvalet. På samma sätt, om man först plockar bort Benjamin kan man bilda C(9, 4) sällskap utan honom. Totalt har man alltså 2 × C(9, 4) möjligheter. Eller, med en annan notation:
B. Båda ska bort
Om man först plockar bort både Amanda och Benjamin kan man av de återstående åtta personerna bilda C(8, 4) sällskap. Men då har man ju inte räknat med de möjligheter där någon (endast en) av de två ovännerna ingår. Hur många sådana finns? Jo, om man i stället för att plocka bort Amanda börjar med att bestämma sig för att hon ska ingå i sällskapet, då har man bara tre personer kvar att välja. Men inte av nio återstående personer, utan av åtta - eftersom Benjamin då inte får väljas. Alltså har man C(8, 3) möjligheter. På samma sätt med Benjamin: det finns C(8, 3) möjligheter att välja ett sällskap där han garanterat ingår och där Amanda garanterat inte ingår. Vi har nu alltså först räknat de sällskap där ingen av ovännerna ingår; sedan de sällskap där Amanda ingår (men inte Benjamin); och slutligen de sällskap där Benjamin ingår (men inte Amanda). Har vi räknat alla möjligheter då? Ja, det har vi. Alltså:
Bry dig inte om hur vi får fram värdet 182 just nu. Det kommer vi till längre fram. Det viktiga nu är själva resonemanget, och att det skiljer sig från det resonemang vi förde i A.
C. Ingen ska bort (förrän i efterhand)
Hur många möjligheter finns om man inte bryr sig om att plocka bort någon av ovännerna? Jo, C(10, 4) Då har man alltså räknat alla möjliga sällskap, även dem där både Amanda och Benjamin ingår. Och de måste ju räknas bort. Så hur många är de? Låt oss räkna "baklänges": Alla de möjliga sällskap där båda ovännerna ingår skulle vi kunna bilda genom att först välja ut just dessa två och bestämma att de ska ingå. Då saknas två personer för att sällskapet ska bli fulltaligt. På hur många sätt kan vi då välja dessa två, av de åtta personer som då återstår? Jo, C(8, 2). Nu har vi först räknat alla möjliga sällskap, och sedan dragit bort dem som inte fungerar:
Vi får samma svar i både B och C, vilket är uppmuntrande. Vilken av dessa två tycker du verkar rimligast? Båda? Ingen? Känns någon av dem rimlig, men fortfarande inte helt övertygande? Eller är båda helt övertygande? Och undrar du i så fall hur det kan vara så? Blir du kanske lite misstänksam?
Hur är det med lösning A? Den ger svaret:
Aj då... Är det något fel? Eller är det kanske B och C som innehåller något fel? Hur kan vi veta det?
Vi tittar på A igen. Vi har räknat alla de sällskap där Amanda inte ingår, och alla de sällskap där Benjamin inte ingår. Det är väl bra? Finns det några fler? Nej, det gör det väl inte...
Eftersom vi nu har två alternativa lösningar att jämföra med, som båda ger samma svar, och som dessutom ger ett lägre svar, kan vi kanske börja misstänka att vi i A har räknat med för många möjligheter.
A'. En ska bort, men bara en
Alla sällskap där Amanda inte ingår, och alla sällskap där Benjamin inte ingår... Hur är det med de sällskap där ingen av dem ingår? De ingår ju både i mängden av sällskap som inte innehåller Amanda och i mängden av sällskap som inte innehåller Benjamin. (Det kan man se om man t.ex. ritar upp ett s.k. Venn-diagram.) Vi har alltså räknat med dem två gånger när vi lade ihop de sällskap som garanterat inte innehöll en av ovännerna. Vi måste alltså dra bort dem en gång. Hur många möjliga sällskap innehåller inte någon av ovännerna? Det räknade vi ut i B: C(8, 4). Vårt nya lösningsförslag blir alltså:
(Hur kommer man att tänka på detta? Hur kan man lära sig att komma på sådana här saker? Kan man lära sig det?)
(I facit till Mattekampen ges C som lösningsförslag.)
Vilken lösningsmetod hade du valt? Om du hade valt A, hade du då kommit fram till A' ?
Vad hade du gjort om du inte sedan tidigare varit bekant med notationen C(n, k)? Jag tror att det då hade varit mycket svårt, men inte omöjligt, för dig att lösa problemet.
---
Låt oss titta närmare på notationen C(n, k) På hur många sätt kan man välja ut k föremål ur en mängd av n stycken föremål? Alla föremål är unika (d.v.s. det går att göra skillnad på dem). Men det spelar ingen roll i vilken ordning de väljs ut.
Ett exempel: Du har fem inramade foton på dina barn och ska ge bort två av dessa till svärmor i julklapp. På hur många sätt kan du välja ut två av fem foton? (Notera att det spelar ingen roll i vilken ordning du väljer ut dem; det enda viktiga är vilka foton svärmor får.)
Tänk dig att du lägger de fem fotona framför dig på en rad. Det första fotot du väljer kan då vara vilket som helst av de fem. Låt säga att du tar bort detta foto från raden och lägger det i ett paket. Kvar ligger nu fyra foton. Du ska välja ett till, och du har nu fyra möjligheter. Du tar bort ytterligare ett foto, vilket som helst, från raden och placerar det i paketet. Nu är svärmors julklapp klar.
På hur många olika sätt skulle den här scenen kunna utspela sig? Det första fotot kan vara vilket som helst av de fem som ligger framme. Nästa foto kan vara vilket som helst av de fyra återstående. För var och en av de fem första scenariorna, finns det fyra fortsättningar. Du har alltså 5 × 4 = 20 möjligheter att välja ut två foton till svärmor.
Men vänta! För svärmors del spelar det ju ingen roll i vilken ordning du har valt ut fotona. Det enda hon är intresserad av är vilka foton som ligger i paketet. I ett av de tjugo scenariorna ovan väljer du först foto X och därefter foto Y. I ett annat scenario väljer du först foto Y och sedan foto X. Av de tjugo scenariorna är alltså hälften likvärdiga, ur svärmors synvinkel. Det finns alltså bara 20/2 = 10 unika julklappar.
Ovanstående sammanfattar vi så här:
Vilket alltså säger att det finns 10 unika urval av två föremål ur en samling på fem föremål.
Hur många unika julklappar kan svärmor få om paketet innehåller tre, i stället för två, foton? Som tidigare resonerar vi först att det finns 5 × 4 × 3 olika sätt att välja ut de tre fotona.
Sedan måste vi ta hänsyn till att en del av dessa resulterar i samma urval av foton. På hur många sätt kan t.ex. foto X, Y, och Z hamna i samma paket? Jo, X skulle kunna hamna i paketet genom att bli utvalt först, men det skulle också kunna hamna i paketet som nummer två i ordningen, eller som nummer tre. Det finns alltså tre möjligheter för foto X att ingå i paketet. Om foto X väljs ut först, kan foto Y väljas antingen som andra eller som tredje foto i ordningen. För varje plats i ordningen som X får, finns alltså två platser kvar till foto Y. Därefter är den kvarvarande platsen för foto Z bestämd. Det finns alltså 3 × 2 paket som alla innehåller just fotona X, Y och Z. (3 × 2 × 1 om man ska vara noga.)
Alltså, hur många unika julklappar kan svärmor få om vi väljer ut tre foton av fem? Jo:
Ja, svaret blir faktisk detsamma som när vi endast valde ut två foton, vilket kanske kan tyckas lite märkligt. C(5, 3) = C(5, 2). Generellt gäller att C(n, k) = C(n, (n-k)), vilket kanske blir klarare om du läser vidare.
---
Nu har vi dels sett hur notationen C(n, k) kan användas, utan att vi bryr oss om det numeriska värdet; dels har vi sett hur man faktiskt tar fram ett numeriskt värde på det som representeras. Vi skall slutligen titta på en generell definition:
I vårt exempel får vi alltså:
Den här definitionen utnyttjar en annan definition, nämligen den av fakultet (!)
I vårt exempel:
Om vi kombinerar dessa definitioner kan vi härleda vårt ursprungliga uttryck:
---
Det verkar osannolikt att någon utan kunskap om dessa metoder skulle lyckas utveckla dem på egen hand, i samband med att man griper sig an det ursprungliga problemet (middagssällskapen). Så utan förkunskaper är uppgiften helt enkelt mycket svår. Men vad det är som gör uppgiften frustrerande även med tillgång till de här metoderna?
Efter introspektion, och efter att ha pratat med en handfull matematiklärare, tror jag att det beror på två saker:
(a) Det finns ingen given lösningsmetod
(b) Man vet inte när, eller om, man är färdig
Det första skälet är intressant, på minst två sätt. Först och främst för att det exemplifierar ett problem, så som detta ofta definieras i matematikundervisning. Enligt den nya skolreformen (Gy11) ska utvecklingen av problemlösningsförmåga nu prioriteras i matematikundervisningen på grundskola och gymnasium. Jag deltar själv just nu i en fortbildning kallad Matematiklyftet, som just syftar till att lära mig (som matematiklärare) att lära mina elever att (utveckla sin förmåga att) lösa problem. Jag är inte säker på att jag kan det. Faktum är att den enda metod jag kan komma på är denna:
Jag tror nämligen inte att man kan befinna sig i en totalt obekant situation. Alternativt att om man kunde det, så skulle man inte ha något verktyg (annat än slumpen) att hantera detta. Man skulle inte kunna förbereda sig för det.
Om man delar mina tvivel på möjligheten att lösa - eller ens råka ut för - genuina "problem", enligt ovanstående definition, blir det intressant att fundera över vad man då kan mena med att det inte finns någon given lösningsmetod. Mitt svar blir att detta i så fall endast innebär att man är relativt ovan vid just den typ av problem (uppgift) som man ställs inför.
Detta innebär i sin tur att det inte finns någon väsensskillnad mellan uppgifter inom diskret matematik och uppgifter inom andra grenar av matematik som är betydligt vanligare i skolan. Det rör sig i stället om en gradskillnad, och denna förklaras helt av den utsträckning i vilken man exponeras för uppgiftstypen.
Det här med att inte veta om (när) man är färdig, det är ju något som är vanligt överallt utom i den traditionella skolmatematiken. Förmåga att hantera sådana situationer är också det ett prioriterat område för skolan - både före och efter den senaste reformen. Och det är betydligt lättare att lära ut än den mytomspunna problemlösningsförmågan. Här kan vi dessutom arbeta tillsammans över ämnesgränserna, utan problem.
Det handlar om att vara kritisk till sina egna och andras förslag, att utsätta dem för systematisk (!) prövning, att söka upp alternativ, att bjuda in och värdera kritik, m.m. Att vara skeptisk och konstruktiv samtidigt. Och social.
Att ta sig an kombinatoriska problem med friskt mod är kanske en god indikator både på hur väl skolan tillämpar, såväl som ingjuter, Kaizen.
Det första skälet är intressant, på minst två sätt. Först och främst för att det exemplifierar ett problem, så som detta ofta definieras i matematikundervisning. Enligt den nya skolreformen (Gy11) ska utvecklingen av problemlösningsförmåga nu prioriteras i matematikundervisningen på grundskola och gymnasium. Jag deltar själv just nu i en fortbildning kallad Matematiklyftet, som just syftar till att lära mig (som matematiklärare) att lära mina elever att (utveckla sin förmåga att) lösa problem. Jag är inte säker på att jag kan det. Faktum är att den enda metod jag kan komma på är denna:
Stoppa så många tekniker som möjligt i ryggsäcken, och titta på så många exempel som möjligt på hur och när dessa tekniker kan användas, så att du i en (relativt) obekant situation ger dig själv goda möjligheter att se (hitta) ett lämpligt "Heureka"-steg.
Jag tror nämligen inte att man kan befinna sig i en totalt obekant situation. Alternativt att om man kunde det, så skulle man inte ha något verktyg (annat än slumpen) att hantera detta. Man skulle inte kunna förbereda sig för det.
Om man delar mina tvivel på möjligheten att lösa - eller ens råka ut för - genuina "problem", enligt ovanstående definition, blir det intressant att fundera över vad man då kan mena med att det inte finns någon given lösningsmetod. Mitt svar blir att detta i så fall endast innebär att man är relativt ovan vid just den typ av problem (uppgift) som man ställs inför.
Detta innebär i sin tur att det inte finns någon väsensskillnad mellan uppgifter inom diskret matematik och uppgifter inom andra grenar av matematik som är betydligt vanligare i skolan. Det rör sig i stället om en gradskillnad, och denna förklaras helt av den utsträckning i vilken man exponeras för uppgiftstypen.
Det här med att inte veta om (när) man är färdig, det är ju något som är vanligt överallt utom i den traditionella skolmatematiken. Förmåga att hantera sådana situationer är också det ett prioriterat område för skolan - både före och efter den senaste reformen. Och det är betydligt lättare att lära ut än den mytomspunna problemlösningsförmågan. Här kan vi dessutom arbeta tillsammans över ämnesgränserna, utan problem.
Det handlar om att vara kritisk till sina egna och andras förslag, att utsätta dem för systematisk (!) prövning, att söka upp alternativ, att bjuda in och värdera kritik, m.m. Att vara skeptisk och konstruktiv samtidigt. Och social.
Att ta sig an kombinatoriska problem med friskt mod är kanske en god indikator både på hur väl skolan tillämpar, såväl som ingjuter, Kaizen.
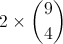











Inga kommentarer:
Skicka en kommentar